머신러닝(ML)

• KNN
• Decision Tree
• SVM
• 선형회귀분석
• 로지스틱회귀분석
• 나이브베이지안

차원의 저주

• 차원(feature)이 증가하면 성능이 저하된다

  • 차원이 증가할수록 말 그대로 ‘근접 이웃’에 한정하기 어려워 멀리 떨어진 데이터를 참조한다

  → 따라서 데이터 양에 비해 feature의 수가 많으면 차원의 저주 문제를 생각해봐야 한다.

• 차원의 저주를 벗어날 수 있는 방법:

  1. 차원 축소(feature 축소)
  2. 데이터 양을 늘림

• 차원의 저주를 벗어날 수 있는 모델

  1. 중요도 분석(의사결정나무 – 사전 가지치기)
  2. PCA 주성분 분석

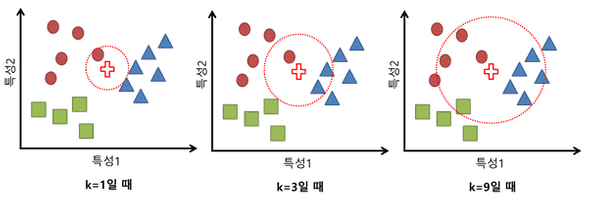
kNN(k-Nearest Neighbor)

Model = `KNeighborsClassifier(~~)`
Grid search:
    n_neighbors=5
    p=2
    meric = ‘minkowski’

• 지도학습

• 테스트 데이터에서 k개의 가장 가까운 이웃을 찾고, 그 이웃들 중 다수가 속한 클래스가 테스트 데이터의 클래스가 되게 한다

  • iris 패키지: “새로운 꽃이 발견됐을 때, 어느 종류(클래스)에 넣는 것이 좋을까?
• 레이지 러닝(lazy learning): 미리 학습해 두는 방식이 아니라, test data 추정할 때마다 학습하기 때문에 시간이 오래 걸림

그림 출처: 심교훈. "유유상종의 진리를 이용한 분류 모델, kNN(k-Nearest Neighbor)"

• K 가 작을수록 복잡도 높아짐

  → 과잉적합

• K가 증가할수록 정확도가 떨어진다

• 거리 측정 방법:

  1. 맨하튼 거리: 가장 심플
  2. 유클리디안 거리: 최단 거리
  3. 민코우스키 거리: 많이 떨어진 성분 부각

결정 트리(Decision Tree)

Model = DecisionTreeClassifier(~~)
- grid search: 
    criterion=’gini’
    알파(가중치)
    max_depth=k
    pd.Categorical(income[c]).codes
    dt.feature_importances ← 중요도 분석
    path = `DecisionTreeClassifier().cost_complexity_pruning_path(trainX, trainY)
    ccp_alpha = ccp_alpha
    * 이때 먼저, ccp_alpha = `ccp_alphas[np.where(ccp_alphas > 0.001)]`
    clfs[-1].tree_.node_count / clfs[-1].tree_.max_depth

• 지도학습, 비지도학습
• 알파값(가중치 조정) 높이기 ~ 오분류율(불순도) 증가

• 핵심: 변별력이 좋은 질문을 위에서부터 하나하나 세팅

  
  
• Feature가 3개 이상이면 초평면으로 구분
• Featrue(차원)이 많아져도 덜 중요한 feature는 분류 기준에서 제외되어 feature 선정에 크게 신경 쓸 필요 X

• 중요한 Feature 확인 가능

  • 중요도 분석
    

• Tree 과도하게 분할( = 과잉 적합 = 트리가 복잡) → 아래 노드에 데이터 小 → 데이터 단편화 → 유의미한 결정 내리기 어려움

  • 즉, Depth 높 ~ 트리 길어짐 ~ 과도하게 분할 ~ overfitting ~ 정확도 낮음
  • 해결 위해 정지기준 or 사전/사후 가지치기 사용

  • 정지기준: depth 지정 or 마지막 노드의 데이터 수가 임계치 이하로 떨어지지 않도록 지정

    • 알파(가중치): depth 조정

  • 가지치기: 트리 단순화하여 일반화 특성 향상시키기.

    1. 사전 가지치기: depth, 마지막 노드의 최소 데이터 수, 불순척도(criterion)
    2. 사후 가지치기: 오분류율, 패널티항, 알파(가중치)
    
    
• ID3 알고리즘: 정보량과 엔트로피 개념 활용

• 알고리즘 순서:

  1. 엔트로피 계산량에 의해 엔트로피(E)가 낮고,
  2. 정보획득량(IG)가 높은 선택지를 선택함
  3. A 속성은 마지막에도 결정 노드에 쓰이지 않았다. N개의 속성 중에 가장 변별력이 낮은 속성이었던 이유다.
• 불순척도(지니지수, 엔트로피) 작아지도록 분할 기준 선택. 분할 전 부모노드 보다 분할 후 자식노드의 불순척도가 작아지는 게 좋음(IG)
• 지니지수: 0~0.5값
• 정보량: 어떤 사건이 가지고 있는 정보의 양. 드물게 발생하는 일일수록 정보량이 크다.

• 엔트로피(E): 0~1값 정보량의 기댓값(평균). 발생한 사건들의 정보량을 모두 구해서 (가중)평균

  • 엔트로피가 크다는 것은 평균정보량이 크다는 것
  • 대개 사건들이 일어날 확률이 비슷한 경우에 엔트로피가 크다.
  • 따라서 두 사건이 0.5, 0.5 확률로 일어날 때의 엔트로피가 가장 크다

  → 즉, 불확실성이 클수록 엔트로피가 크다

  → 불확실성이 크면 클수록 분류하기는 어려워짐

  → 엔트로피가 가장 작은 것을 상위 의사결정 노드에 위치시켜야 함.

  → 이를 위해 정보획득량(IG)이란 개념이 필요

  "어떤 속성을 가지고 분류했을 때 가장 엔트로피(불확실성)가 작은지, 정보획득량이 큰지"

서포트 벡터 머신(SVM)

Model = SVC(~~)
grid search : 
    kernel = ‘linear’
    C
    gamma
    (비선형+multiclassification) kernel = `‘rbf’
     * 파라미터 C는 이상치 또는 오류를 얼마나 허용하는 가(복잡도 조절)를 정해주고, gamma는 결정 경계의 곡률을 결정
        * C: max margin + min 섞임 조절
        * C: 大 ~ 패널티항 大 ~ 거리 짧음

• 가장 많이 사용되는 SVM은 radial(방사형) basis function (RBF) 커널을 사용한 SVM
• SVM은 일반화 특성이 우수

• 모델 생성시 특정 옵션을 주어야 predict_proba가 사용 가능

  predict_proba 함수를 가지고 있지만, 모델 생성시 probalility=True를 설정하지 않으면 사용할 수 없다.

  이때, 레이블이 3개 이상인 경우, LinearSVC보단 SVC를 사용하고, probability=True 옵션 주는 것을 추천한다.

  출처: mathcom. "Scikit-learn에서 predict_proba 및 AUC 계산하기"

선형 SVM

• 데이터를 선형으로 분리하는 최적의 선형 결정 경계를 찾는 알고리즘

  • 그 중 가장 간단한 것이 선형 SVM(linear SVM)
  
  

• SVM 알고리즘의 목표: 클래스가 다른 데이터들을 가장 큰 마진(margin)으로 분리해내는 선 또는 면(결정 경계 또는 분리 초평면)을 찾아내는 것

  • 마진: 두 데이터 군과 결정 경계와 떨어져있는 정도
  • 서포트 벡터: 결정 경계와 가장 먼저 만나는 데이터
  
  
• SVM의 기본 매개변수인 C

• cost(C): C는 얼마나 많은 데이터 샘플이 다른 클래스에 놓이는 것을 허용하는지를 결정

  ex: 작을 수록 많이 허용, 클 수록 적게 허용 ex: C값을 낮게 설정하면 이상치들이 있을 가능성을 크게 잡아 일반적인 결정 경계를 찾아내고, 높게 설정하면 반대로 이상치의 존재 가능성을 작게 봐서 좀 더 세심하게 결정 경계를 찾아낸다. ex: "난 데이터 샘플하나도 잘못 분류할 수 없어!" : C를 높여야 ex: "몇 개는 놓쳐도 괜찮아, 이상치들이 꽤 있을 수도 있으니까" : C를 낮춰야

  출처: 심교훈. "서포트 벡터 머신(SVM)의 사용자로서 꼭 알아야할 것들 - 매개변수 C와 gamma"

• C가 너무 낮으면 과소적합(underfitting)

• C가 너무 높으면 과대적합(overfitting)

  → 적합한 C값을 찾아내는 것이 중요

• 하드마진(hard-margin) SVM
• 소프트마진(soft-margin) SVM

RBF 커널 SVM

• 커널 기법은 주어진 데이터를 고차원 특징 공간으로 사상해주는 것이다.
• 3차원 공간에서 분류된 것을 다시 2차원 공간으로 매핑해서 보면 결정 경계가 둥그렇게 보일 것

• RBF 커널의 경우 gamma라는 매개변수를 사용자가 조정해야 한다.

  • gamma : 하나의 데이터 샘플이 영향력을 행사하는 거리를 결정
  • ex: gamma가 클수록 한 데이터 포인터들이 영향력을 행사하는 거리가 짧아지는 반면, 낮을수록 커진다

  • ex: gamma는 가우시안 함수의 표준편차와 관련되어 있는데, 클수록 작은 표준편차를 의미

    • '편차가 크다': 어떤 자료는 평균보다 엄청 크고 어떤 자료는 평균보다 엄청 작다

• gamma 매개변수는 결정 경계의 곡률을 조정한다고 말할 수도 있다.

  • gamma의 값이 높아짐에 따라 공간이 점점 작아지는데, 위에서 언급한 것과 같이 각각의 데이터 포인터가 영향력을 행사하는 거리가 짧아졌기 때문 <- 아마 정확도가 높아질 듯하다.

• 매개변수 C와 마찬가지로 너무 낮으면 과소적합될 가능성이 크고, 너무 높으면 과대적합의 위험이 있다.

  • 두 값 모두 커질수록 알고리즘의 복잡도는 증가하고, 작아질수록 복잡도는 낮아진다.
  
  

선형 회귀(linear regression)

Model = LinearRegression()

• 예측값(Y햇)이 실수(연속형)일 떈, ‘.mean’, ‘.score’ 말고 R2(*0~1값을 가짐) 사용(값의 범위가 MSE보다 작기 때문)

• 선형회귀는 사용되는 '특성(feature)의 개수'에 따라

  1. 단순 선형 회귀(simple linear regression): 단 하나의 특징(feature)을 가지고 라벨값(label) 또는 타깃(target)을 예측하기 위한 회귀 모델을 찾는다.
  2. 다중 선형 회귀(multiple linear regression): 하나의 특성이 아닌 여러 개의 특성을 활용해서 회귀모델을 만듦
• 선형 회귀는 y와 y햇 사이의 평균제곱오차(mean squared error, MSE)를 최소화하는 파라미터(w, b)를 찾는다. y와 y햇의 차이가 작으면 작을 수록 예측 성능이 좋기 때문
• 라쏘(Lasso): 선형 회귀의 단점을 극복하기 위해 개발된 방법
• linear regression에선 predict_proba 함수를 제공하지 않는다

• y햇 = w[0]+x[0]+b

  • w: 가중치(weight), 계수(coefficient)
  • b: 편항(offset)
  • y햇: 예측값
  • x[0]: 특징
  • "feature와 lable 사이의 관계를 잘 설명해낼 수 있는 최적(가장 적합한)의 w와 b를 찾는 것"

라쏘(L1)

• 추가 제약조건이자 grid search
• 선형 회귀에 L1 규제를 줘서 과대적합을 피하는 방법이다.
• 상관성이 있을 수도 있는 feature의 영향력을 줄일 수 있음

• 동작 원리:

  • MSE가 최소가 되게 하는 w, b 찾기 + w의 모든 원소가 0이 되거나 0에 가깝게
  • MSE와 penalty 항의 합이 최소가 되게 하는 w와 b를 찾는 것이 라쏘의 목적

• L1-norm(벡터의 요소들의 절대값들의 합) 패널티를 조정하는 건 알파값(선형회귀 분석의 grid serch)

  • 알파 너무 작으면 과대적합(복잡도 큼), 너무 크면 과소 적합(복잡도 넘 작음)

• 라쏘의 장점:

  1. 제약 조건을 통해 일반화된 모형을 찾는다.
  2. 모델 해석력이 good (모델에서 가장 중요한 특성이 무엇인지 아는)

릿지(L2)

• L2-norm
• 릿지 원의 크기와 라쏘의 마름모 크기는 정규화 역할하는 람다 혹은 C로 조절
• 특성이 다수일 경우에는 릿지 회귀가 좀 더 잘 작동. 선형 회귀와 달리 모델의 복잡도를 조정할 수 있기 때문. 복잡도를 조정할 수 있다는 말은 사용자가 설정 가능한 파라미터가 있다는 뜻
• 알파값(가중치): (feature가 생각보다 덜 쓰였다던가의)과소적합: 1보다 작은 α 값(ex: 0.1, 0.01, 0.001)로 조정

• 즉, alpha 값을 크게 설정 ~ 기울기가 줄어듦 ~ 특성들이 출력에 미치는 영향력이 줄어듦(현재 특성들에 덜 의존)

  • alpha = 0 ← 선형회귀
  • default : alpha = 1

• 정리

  • 특성이 많은데 그중 일부분만 중요하다면 라쏘
  • 특성의 중요도가 전체적으로 비슷하다면 릿지

로지스틱 회귀 분석

model = Logisticregression(~~)
grid search:
    penaly = ‘l2’
    C = c
    max_iter = 500

• 선형회귀분석에서 쓰던 MSE 말고 Cross Entropy(CE) 사용
• 오즈(0.9가 나왔으면 1이라 보는 것)

• 계산 시 유의 사항:

  • 예측값(y햇)이 실제값(y)과에 가깝게 나오게 하기 위해 CE, MSE 최소화
  • 출력에 1이 여러 개인(sigmoid 출력) 이진분류일 경우 BCE(바이너리 CE) 사용: 개별 출력이라 1이 여러 개
  • 출력에 1이 한 개일 경우(one-shot 형태로 softmax가 출력) CCE(카테고리컬 CE) 사용: 그룹(?) 출력이라 1이 하나

  → BCE, CCE는 결과가 다르고 정확도 측정도 달라지므로 주의해서 선택

  
  

• sklearn 패키지에서는 sigmoid 안 거치고 바로 softmax로 감

  
  

• 보통의 계산 순서:

  1. sigmoid 함수로 계산
  2. softmax함수로 계산(이때 CE 사용)

• 로지스틱함수의 yHat 계산법(step):

  1. 시그모이드 계산
  2. 시그모이드(sigmoid) 함수: 가중치와 바이어스는 시그모이드의 비활성도를 조절해준다.
  3. CE 계산

나이브 베이지안

• model = GaussianNB()
• Feature들이 서로 독립이라 가정하고 조건부 확률 계산해서 데이터 분류

• 명목형(1, 0), 연속형(정규분포 사용) 변수 모두 사용 가능

  
  

• 계산 순서:

  1. 결합 확률은 너무 복잡해서 두 feature를 독립이라 가정하여,
  2. 베이지안 식에 의해 각각을 곱해 계산한 후,
  3. 큰 확률의 값을 선택

  Ex: yes 일 확률 : 1 , no일 확률: 0 => (계산 후) no로 분류

  
  
• m 추정치(m-Estimates): 비교하려는 두 샘플의 data 중에 특정 데이터가 없을 땐 두 확률이 모두 0으로 나와서 분류할 수 없으므로, m-Estimates라는 m과 p를 사용해서 조건부 확률 계산식을 조정함.
• 분모의 m은 임의의 확률, mp는 분자가 0 나오는 거 방지

• 명목형, 연속형 모두 섞여 있는 data 일 땐,

  1. 명목형, 연속형 각각 model 학습
  2. 각각의 model 정확도 추정
  3. '2'의 그 정확도(확률)을 곱함
  4. '3'의 확률의 곱으로 정확도 측정

참고:

• 심교훈. 019. 10. 24. "결정 트리(Decision Tree) 알고리즘, ID3 소개". https://bskyvision.com/598. b스카이비전.
• 심교훈. 2020. 1. 20. "[ubuntu+python] 선형 회귀의 업그레이드 버전1, 릿지 회귀". https://bskyvision.com/687. b스카이비전
• 심교훈. 2017. 10. 21. "서포트 벡터 머신(SVM)의 사용자로서 꼭 알아야할 것들 - 매개변수 C와 gamma". https://bskyvision.com/163. b스카이비전.
• 머신러닝. 2020.01.14. "서포트 벡터 머신(Support Vector Machine) 쉽게 이해하기". http://hleecaster.com/ml-svm-concept/. 아무튼워라밸
• mathcom. 2018. 09. 14. "Scikit-learn에서 predict_proba 및 AUC 계산하기". https://m.blog.naver.com/cjh226/221358912619. Notepad for mathcom