one-hot 인코딩
- categorical 변환 방법
keras
-
Keras를 이용한 one-hot encoding
data = ['남자', '여자', '아빠', '엄마', '삼촌', '이모'] values = np.array(data) print(values) print(sorted(values))['남자' '여자' '아빠' '엄마' '삼촌' '이모'] ['남자', '삼촌', '아빠', '엄마', '여자', '이모']
from tensorflow.keras.utils import to_categorical encoded = to_categorical(integer_encoded) print(encoded)[[1. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0.] [0. 0. 1. 0. 0. 0.] [0. 0. 0. 1. 0. 0.] [0. 1. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 1.]]
sklearn
-
sklearn의 preprocessing을 이용한 one-hot encoding 방법
data = ['남자', '여자', '아빠', '엄마', '삼촌', '이모'] values = np.array(data) print(values) print(sorted(values))['남자' '여자' '아빠' '엄마' '삼촌' '이모'] ['남자', '삼촌', '아빠', '엄마', '여자', '이모']
- label 인코딩 필요
import sklearn.preprocessing as sk label_encoder = sk.LabelEncoder() integer_encoded = label_encoder.fit_transform(values) print(integer_encoded)[[0] [4] [2] [3] [1] [5]]
- OneHotEncoding
# integer encoding print(integer_encoded) # binary encoding integer_encoded = integer_encoded.reshape(len(integer_encoded), 1) onehot_encoder = sk.OneHotEncoder(sparse=False, categories='auto') onehot_encoded = onehot_encoder.fit_transform(integer_encoded) print(onehot_encoded)[[1. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0.] [0. 0. 1. 0. 0. 0.] [0. 0. 0. 1. 0. 0.] [0. 1. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 1.]]
-
단점: OOV 문제
- 해결을 위한 노력: 페이스북의 FastText
Hash
Indexing
- 예) 견출지
- SQL의 내부 알고리즘
-
단점: 견출지 붙일 때, 몇 장마다 붙일지 미리 정해야 됨
- Key의 범위가 넓다면 Memory 비효율성
- 장점: 나중에 찾을 때, 빠르다
-
검색 속도는 빠르다
Hashing
- 예) apple이란 단어를 수치변환하여 84 page의 36번째 line에 기록한다
- 다른 단어를 입력할 때, apple에 적용했던 방법을 답습하여 손쉽게 기록할 수 있다
-
단점: collision 발생
- apple과 tiger 단어가 우연히 같은 line에 기록될 수 있다.
- 단점 해결: overflow 처리
-
장점: 메모리 효율성
- 특히 넓은 key 영역에서 효율적이다.
Hashing을 단어 표현에 적용
-
Hashing trick을 위한 word emgedding 방법
- vocabulary 크기를 미리 지정(hash table)하고, 단어들을 hash table에 대응 시키는 방식
-
hash('apple') or md5('apple') % 8 = 1
- '% 8' : 모듈러 연산을 취해준다
- '1' : vetor화 시킨 것 => 1번째 line에 있다
- 현업에선 "collision 발생 확률을 몇 프로로 줄이기 위해 hash table의 크기를 몇으로 둘 것인가?" 에 관해 논의 후 설계하기도 함
- code: 3-2. hashing_trick.py
카운트 기반 방법(Co-occurrence matrix)
- Co-occurrence matrix: 동시 발생(출현) 행렬
- 같이 쓰인 횟수(인접 사용한 횟수)를 matrix에 기록하는 것
- 학습 기반이 아닌 빈도 기반의 단어들 간의 관계 정보(단어 간 유사도)를 내포하고 있다.
- 모든 단어를 vocabulary라고 할 때, one-hot의 size(개수) = vocabulary의 size(개수) = 단어 벡터
-
one-hot 인코딩이 아니다.
- 예) 0 0 0 2 1 0 0 0
- 대칭 행렬, 희소 행렬('0'이 많음)
-
긴 단어일수록 차원이 크다
- SVD(특이값 분해)를 사용해 단어 벡터의 차원을 줄일 수 있다.
- 약 25% 정도 줄일 수 있다.
- vocab 사이즈를 줄이고 embedding layer에 쓴 것처럼.
-
(Documnet Term Freq 2개) Xt와 X의 곱행렬을 하면, 일일이 빈도를 구하지 않아도 문장 간 공통된 단어가 쓰인 횟수를 행렬로 만들 수 있다.
- 그렇게 만들어진 행렬이 Co-occurrence matrix
- 그렇게 만들어진 행렬이 Co-occurrence matrix
-
Unigram(1단어), Bigram(2단어)까지 vocab을 만들 수 있다.
- 조합이 더 많아진다.
- 조합이 더 많아진다.
-
Glove:
- 아래 2개의 단점을 고려해 장점을 합친 것
- Co-occurrence matrix: (빈도 기반) 전체 단어를 고려했다.
- Skip-gram: (학습 기반)주변 단어에 한정했다.
- 두 단어를 Embedding layer에 통과시키고(학습기반) 각 vector의 내적의 합(빈도기반)을 구해 거리를 구한다.
- log(P(도서관, 갔다)) = 0.33
- 기계 : 도서관은... 가는 곳이다.... 라고 기계가 인식함
- 단점: 계산량이 많다
특이값 분해(SVD: 차원축소) code
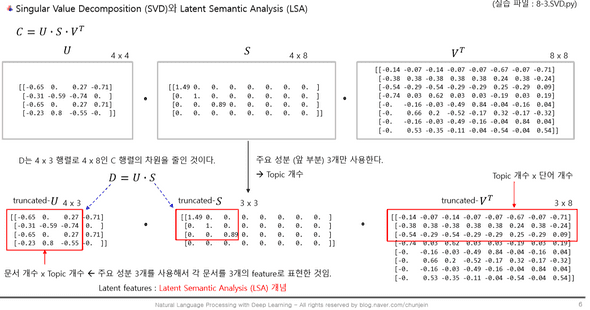
LSA : 잠재 의미 분석
- U, S, VT 행렬의 의미 --> Latent Semantic Analysis (LSA)
- U 행렬 ~ 차원 = (문서 개수 X topic 개수) : 문서당 topic 분포
- S 행렬 ~ 차원 = (topic 개수 X topic 개수) : 대각성분. 나중에 행렬에 넣을 땐 대각성분만 빼면 0
- VT 행렬. 차원 = (topic 개수 X 단어 개수) : topic 당 단어 빈도의 분포
=> 이를 여기선 문장과 단어 사이의 관계로 해석
from sklearn.feature_extraction.text import CountVectorizerdocs = ['성진과 창욱은 야구장에 갔다',
'성진과 태균은 도서관에 갔다',
'성진과 창욱은 공부를 좋아한다']- Vocab 만들기
count_model = CountVectorizer(ngram_range=(1,1)) # gram_range=(1,1): Unigram 단어 1개씩 동시 발생. # CountVectorizer: 문장의 단어를 단어 하나씩 자른단 뜻
x = count_model.fit_transform(docs)- 문서에 사용된 사전을 조회한다.
print(count_model.vocabulary_){'성진과': 3, '창욱은': 6, '야구장에': 4, '갔다': 0, '태균은': 7, '도서관에': 2, '공부를': 1, '좋아한다': 5}
- Compact Sparse Row(CSR) format: 단어별 빈도를 표현한다.
# (row, col) value
print(x)(0, 3) 1 (0, 6) 1 (0, 4) 1 (0, 0) 1 (1, 3) 1 (1, 0) 1 (1, 7) 1 (1, 2) 1 (2, 3) 1 (2, 6) 1 (2, 1) 1 (2, 5) 1
- 행렬 형태로 표시한다. (Document-Term Freq)
print(x.toarray())
print()
print(x.T.toarray())print(x.toarray()) >
[[1 0 0 1 1 0 1 0] [1 0 1 1 0 0 0 1] [0 1 0 1 0 1 1 0]]
print(x.T.toarray()) >
[[1 1 0] [0 0 1] [0 1 0] [1 1 1] [1 0 0] [0 0 1] [1 0 1] [0 1 0]]
- x.T의 의미 > 1 2 3 - 문장 갔다 [[1 1 0] - '갔다'라는 단어는 문장-1과 문장-2에 쓰였음. 공부를 [0 0 1] - '공부를'은 문장-3에만 쓰였음. 도서관에 [0 1 0] 성진과 [1 1 1] 야구장에 [1 0 0] 좋아한다 [0 0 1] 창욱은 [1 0 1] 태균은 [0 1 0]]
xc = x.T * x # this is co-occurrence matrix in sparse csr format
xc.setdiag(0) # sometimes you want to fill same word cooccurence to 0
print(xc.toarray())
0
갔다1
공부를2
도서관에3
성진과4
야구장에5
좋아한다6
창욱은7
태균은0 갔다 0 0 1 2 1 0 1 1 1 공부를 0 0 0 1 0 1 1 0 2 도서관에 1 0 0 1 0 0 0 1 3 성진과 2 1 1 0 1 1 2 1 4 야구장에 1 0 0 1 0 0 1 0 5 좋아한다 0 1 0 1 0 0 1 0 6 창욱은 1 1 0 2 1 1 0 0 7 태균은 1 0 1 1 0 0 0 0
-
참고 > ngramrange(minn = 1, max_n = 2)인 경우
- 즉, ngram_range=(1,2):unigram과 bigram 둘다 동시에 조회하는 경우
-
count_model = CountVectorizer(ngram_range=(1,2)) x = count_model.fit_transform(docs) # 문서에 사용된 사전을 조회 print(count_model.vocabulary_) xc = x.T * x # this is co-occurrence matrix in sparse csr format xc.setdiag(0) # sometimes you want to fill same word cooccurence to 0 print(xc.toarray()){'성진과': 5, '창욱은': 11, '야구장에': 8, '갔다': 0, '성진과 창욱은': 6, '창욱은 야구장에': 13, '야구장에 갔다': 9, '태균은': 14, '도서관에': 3, '성진과 태균은': 7, '태균은 도서관에': 15, '도서관에 갔다': 4, '공부를': 1, '좋아한다': 10, '창욱은 공부를': 12, '공부를 좋아한다': 2}
[[0 0 1 2 1 0 1 1] [0 0 0 1 0 1 1 0] [1 0 0 1 0 0 0 1] [2 1 1 0 1 1 2 1] [1 0 0 1 0 0 1 0] [0 1 0 1 0 0 1 0] [1 1 0 2 1 1 0 0] [1 0 1 1 0 0 0 0]]
변수 정리 > x / x.T / xc
- x: 단어별 빈도
- x.T: Sparse 해주려고 x를 transpose함
-
xc : x와 x.T의 곱행렬이자, 처음에 쓸 땐 co-occurrence matrix 만들기 위한 csr 형태.
- 여기에
- xc.setdiag(0) 해주고,
- xc.toarray() 해주면
- co-occurrence matrix 완성
numpy를 이용한 SVD 예시
- Co-occurrence matrix를 SVD로 분해한다.
- C = U , S, VT
import numpy as np
C = xc.toarray()
U, S, VT = np.linalg.svd(C, full_matrices = True) # np.linalg.svd 써주면 U, S, VT로 자동 분배됨
print(np.round(U, 2), '\n')
print(np.round(S, 2), '\n')
print(np.round(VT, 2), '\n')[[-0.44 -0.39 -0.58 0.41 0.35 0. -0. -0.19] [-0.24 -0.12 0.29 0.41 -0.24 0.65 -0.29 0.35] [-0.24 -0.12 -0.29 -0.41 -0.24 -0.29 -0.65 0.35] [-0.56 0.8 0. -0. 0.19 0. 0. 0.02] [-0.27 -0.01 -0. -0. -0.7 0. -0. -0.66] [-0.24 -0.12 0.29 0.41 -0.24 -0.65 0.29 0.35] [-0.44 -0.39 0.58 -0.41 0.35 -0. 0. -0.19] [-0.24 -0.12 -0.29 -0.41 -0.24 0.29 0.65 0.35]]
[5.27 2.52 1.73 1.73 1.27 1. 1. 0.53]
[[-0.44 -0.24 -0.24 -0.56 -0.27 -0.24 -0.44 -0.24] [ 0.39 0.12 0.12 -0.8 0.01 0.12 0.39 0.12] [-0. 0.5 -0.5 -0. 0. 0.5 -0. -0.5 ] [-0.71 0. -0. 0. 0. 0. 0.71 -0. ] [-0.35 0.24 0.24 -0.19 0.7 0.24 -0.35 0.24] [-0. -0.65 0.29 -0. 0. 0.65 0. -0.29] [-0. 0.29 0.65 -0. 0. -0.29 -0. -0.65] [-0.19 0.35 0.35 0.02 -0.66 0.35 -0.19 0.35]]
-
S를 정방행렬로 바꾼다.
- S
- 정방행렬이므로, 같은 수의 행과 열을 가지는 행렬
- 대각행렬이므로, 대각 성분을 제외한 원소는 모두 0 인 행렬
s = np.diag(S) # s는 대각행렬이자 정방행렬
print(np.round(s, 2))[[5.27 0. 0. 0. 0. 0. 0. 0. ] [0. 2.52 0. 0. 0. 0. 0. 0. ] [0. 0. 1.73 0. 0. 0. 0. 0. ] [0. 0. 0. 1.73 0. 0. 0. 0. ] [0. 0. 0. 0. 1.27 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0.53]]
- A = U.s.VT를 계산하고, A와 C가 일치하는지 확인한다.
A = np.dot(U, np.dot(s, VT))
print(np.round(A, 1))
print(C)[[ 0. 0. 1. 2. 1. 0. 1. 1.] [-0. 0. 0. 1. 0. 1. 1. 0.] [ 1. -0. 0. 1. 0. -0. 0. 1.] [ 2. 1. 1. 0. 1. 1. 2. 1.] [ 1. 0. -0. 1. 0. 0. 1. -0.] [ 0. 1. 0. 1. 0. -0. 1. 0.] [ 1. 1. 0. 2. 1. 1. 0. -0.] [ 1. -0. 1. 1. -0. -0. -0. 0.]]
[[0 0 1 2 1 0 1 1] [0 0 0 1 0 1 1 0] [1 0 0 1 0 0 0 1] [2 1 1 0 1 1 2 1] [1 0 0 1 0 0 1 0] [0 1 0 1 0 0 1 0] [1 1 0 2 1 1 0 0] [1 0 1 1 0 0 0 0]]
sklearn을 이용한 SVD 예시
- Co-occurrence matrix를 SVD로 분해한다.
from sklearn.decomposition import TruncatedSVD- 특이값 (S)이 큰 4개를 주 성분으로 C의 차원을 축소한다.
svd = TruncatedSVD(n_components=4, n_iter=7)
D = svd.fit_transform(xc.toarray()) # fit_transform : 학습 시키고 transpose도 한꺼번에 시킴
U = D / svd.singular_values_ # svd.singular_values_ : 대각 성분의 값
S = np.diag(svd.singular_values_) # np.diag: '대각행렬'로, 대각 성분의 값만을 행렬 형태로 추출한 것. 정방행렬의 형태를 띄고 있음
VT = svd.components_print(np.round(U, 2), '\n') >
[[ 0.44 -0.39 0.41 -0.58] [ 0.24 -0.12 0.41 0.29] [ 0.24 -0.12 -0.41 -0.29] [ 0.56 0.8 -0. 0. ] [ 0.27 -0.01 -0. -0. ] [ 0.24 -0.12 0.41 0.29] [ 0.44 -0.39 -0.41 0.58] [ 0.24 -0.12 -0.41 -0.29]]
print(np.round(S, 2), '\n') >
[[5.27 0. 0. 0. ] [0. 2.52 0. 0. ] [0. 0. 1.73 0. ] [0. 0. 0. 1.73]]
print(np.round(VT, 2), '\n') >
[[ 0.44 0.24 0.24 0.56 0.27 0.24 0.44 0.24] [ 0.39 0.12 0.12 -0.8 0.01 0.12 0.39 0.12] [-0.71 0. -0. 0. 0. 0. 0.71 -0. ] [-0. 0.5 -0.5 -0. 0. 0.5 -0. -0.5 ]]
-
C를 4개 차원으로 축소: truncated (U * S)
- U * S * VT 하면 원래 C의 차원과 동일해 진다.
- U * S가 축소된 차원을 의미하고,
- V는 축소된 차원을 원래 차원으로 되돌리는 역할을 한다 (mapping back)
print(np.round(D, 2))[[ 2.31 -0.97 0.71 -1. ] [ 1.24 -0.3 0.71 0.5 ] [ 1.24 -0.3 -0.71 -0.5 ] [ 2.97 2.03 -0. 0. ] [ 1.44 -0.03 -0. -0. ] [ 1.24 -0.3 0.71 0.5 ] [ 2.31 -0.97 -0.71 1. ] [ 1.24 -0.3 -0.71 -0.5 ]]
변수 정리 > C / D / Vt
- 원래 행렬: C
-
차원축소: D = U*S
- 이때, U, S는 중요한 부분만 추림 U(truncated), S(truncated))
- Vt = S를 기준으로 Vt를 truncated함
SVD : Numpy & sklearn 비교
- Co-occurrence matrix를 SVD로 분해
- 여기서 말하는 '차원 축소': 한 문장 내 다른 문장과 쓰이는 중요 단어만 추출함
| Numpy | sklearn | |
|---|---|---|
| Code | import numpy as np | from sklearn.decomposition import TruncatedSVD |
| > C = U.S.VT C = xc.toarray() U, S, VT = np.linalg.svd(C, full_matrices = True) |
> 특이값 (S)이 큰 4개를 주 성분으로 C의 차원을 축소 svd = TruncatedSVD(ncomponents=4, niter=7) D = svd.fittransform(xc.toarray()) U = D / svd.singularvalues S = np.diag(svd.singularvalues) VT = svd.components |
|
| > S를 정방행렬로 바꾼다. s = np.diag(S) |
||
| > A = U.s.VT를 계산하고, A와 C가 일치하는지 확인 A = np.dot(U, np.dot(s, VT)) |
||
| 특징 | 알아서 주성분을 추출해 차원 축소할 수 있다. | 원하는 수의 주성분으로 차원을 축소할 수 있다. |
- U * S * VT 하면 원래 C의 차원과 동일해 진다.
- U * S가 축소된 차원을 의미하고,
- V는 축소된 차원을 원래 차원으로 되돌리는 역할(mapping back)을 한다
텍스트 유사도(거리 측정)
Step 1. word의 vector화
TfidfVectorizer사용
from sklearn.feature_extraction.text import TfidfVectorizer
sent = ("휴일 인 오늘 도 서쪽 을 중심 으로 폭염 이 이어졌는데요, 내일 은 반가운 비 소식 이 있습니다.",
"폭염 을 피해서 휴일 에 놀러왔다가 갑작스런 비 로 인해 망연자실 하고 있습니다.")
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(sent).toarray()
print(np.round(tfidf_matrix, 3))[[0. 0.324 0. 0. 0.324 0.324 0.324 0.324 0.324 0.324 0. 0.231 0.324 0.231 0. 0. 0.231] [0.365 0. 0.365 0.365 0. 0. 0. 0. 0. 0. 0.365 0.259
- 0.259 0.365 0.365 0.259]]
HashingVectorizer사용
from sklearn.feature_extraction.text import HashingVectorizer
sent = ("휴일 인 오늘 도 서쪽 을 중심 으로 폭염 이 이어졌는데요, 내일 은 반가운 비 소식 이 있습니다.",
"폭염 을 피해서 휴일 에 놀러왔다가 갑작스런 비 로 인해 망연자실 하고 있습니다.")
VOCAB_SIZE = 20 # 사용자가 직접 지정해야 하는 값
hvectorizer = HashingVectorizer(n_features=VOCAB_SIZE,norm=None,alternate_sign=False)
hash_matrix = hvectorizer.fit_transform(sent).toarray()
print(hash_matrix)[[0. 2. 0. 0. 0. 1. 1. 1. 1. 0. 0. 0. 2. 2. 0. 1. 0. 0. 0. 0.] [0. 2. 1. 0. 0. 1. 1. 0. 0. 0. 1. 0. 0. 0. 0. 0. 2. 1. 0. 0.]]
자카드 유사도
- 문장 中 중복되는 단어의 개수를 센다.
- 두 문장에 겹친 단어 개수 / 사전의 전체 단어 개수
-
code
- (수치화(vector)화 안 하고) 문장 간의 겹치는 단어만 세는 것도 가능하다.
sent_1 = set(sent[0].split()) sent_2 = set(sent[1].split()) print(sent_1) print(sent_2) # 합집합과 교집합을 구한다. hap_set = sent_1 | sent_2 # | : or gyo_set = sent_1 & sent_2 # & : and print(hap_set, '\n') print(gyo_set, '\n') jaccard = len(gyo_set) / len(hap_set) print(jaccard){'폭염', '있습니다.', '비', '휴일', '을'}
- (수치화(vector)화 하고) jaccard_score 패키지
count_model = CountVectorizer(ngram_range=(1,1)) # bigram은 ngram_range=(1,2) : (from, to) = 1에서 2까지 x = count_model.fit_transform(sent).toarray() from sklearn.metrics import jaccard_score jaccard_score(x[0], x[1])0.17647058823529413
코사인 유사도
- 코사인 유사도는 클수록 유사도가 높다
- 코사인 거리는 작을수록 거리가 좁다
-
code
from sklearn.metrics.pairwise import cosine_similarity d = cosine_similarity(tfidf_matrix[0:1], tfidf_matrix[1:2]) print(d)[[0.17952266]]
유클리디안 거리
- L2 - Distance
-
code
from sklearn.metrics.pairwise import euclidean_distances euclidean_distances(tfidf_matrix[0:1], tfidf_matrix[1:2])array([[1.28099753]])
맨하탄 거리
- L1 - Distance
- 유클리디안 거리와의 비교: 거리 값은 유클리디안 거리가 작게 나오지만, 대각선의 길을 선택할 수 있다는 건 현실성이 떨어지기 때문에 맨하탄 거리를 선택하는 경우도 있다.
-
code
from sklearn.metrics.pairwise import manhattan_distances d = manhattan_distances(tfidf_norm_l1[0:1], tfidf_norm_l1[1:2])[[0.77865927]]
정규화(l1 & l2)
-
l1- 유클리디안/맨하탄 거리는 '거리'라 값이 1이 넘어갈 수 있기 때문에 가시적인 효과를 위해 0~1 사이의 값을 갖도록 L1 정규화를 수행한 후, 각각의 유클리디안/맨하탄 거리를 수행할 수도 있다.
- 함수
def l1_normalize(v): return v / np.sum(v) tfidf_norm_l1 = l1_normalize(tfidf_matrix) d = euclidean_distances(tfidf_norm_l1[0:1], tfidf_norm_l1[1:2]) print(d)- numpy 패키지
L1_norm = np.linalg.norm(x, axis=1, ord=1) print(L1_norm)
-
l2- l2 + HashingVectorizer 패키지
VOCAB_SIZE = 20 hvectorizer = HashingVectorizer(n_features=VOCAB_SIZE,norm='l2',alternate_sign=False) hash_matrix = hvectorizer.fit_transform(sent).toarray() print(np.round(hash_matrix, 3))-
numpy 패키지
import numpy as np L2_norm = np.linalg.norm(x, axis=1, ord=2) print( L2_norm)
-
참고:
- 아마추어 퀀트, blog.naver.com/chunjein
- 코드 출처 및 내용 공부: 전창욱, 최태균, 조중현. 2019.02.15. 텐서플로와 머신러닝으로 시작하는 자연어 처리 - 로지스틱 회귀부터 트랜스포머 챗봇까지. 위키북스