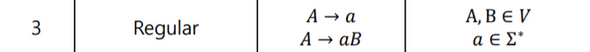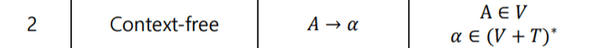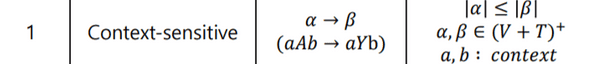title profile picture

JyneeEarth

(NLP 기초) 문장 구조 분석

Jul 17, 2020(Last updated: Aug 16, 2020)
·
Post Series

NLP

  • 형식언어 이론

    • Context-free Grammar
    • Context-sensitive Grammar
    • Natural Language


문장 구조 분석

  • Word-salad(말비빔): 문법적으로는 완벽히 맞지만 의미가 없는 문장

형식언어 이론 : Formal Language Theory

  • 언어란?

    • (형식적 측면) 유한개의 철자로 무한개의 단어와 문장을 조합한 것
    • (의미적 측면) 무한한 의미를 생성할 수 있는 것

  • 촘스키의 계층 구조 (Chomsky Hierarchy)

    • 의미 없이 문장이 형성되는 과정을 형식으로 설명 : 형식언어(formal language theory)
    • groucho_grammar = nltk.CFG.fromstring(""" V와 T로 문법 정의 """)
    • V : Variable
    • T : Terminal
    • image-20200717161151561
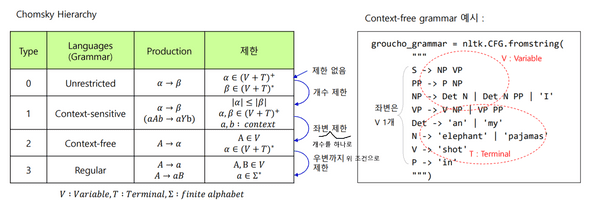
    • derivation: Context-free grammar에서, 우변 → 좌변(Variable, Terminal)일 때 → 하는 과정
    • Unrestricted: 자연어(사람 말)
    • Context-sensitive부터 Regualr까지 오토마타(Automata)



    오토마타(Automata)

    • 어떤 Language가 어떤 Grammar에 따르는지 그래서 Accept할지, Reject할지 Check하는 추상적인 기계(장치)

  • image-20200717161524521

    • Unrestricted(Natural Language)

  • Type-0 : Recognized by Turing Machine

    • Context-sensitive
    • Type-1 : Accepted by Linear Bound Automata
    • Context-free
    • Type-2 : Accepted by Push Down Automata (PDA)
    • Regular
    • Type-3 : Accepted by Finite State Automata (FSA)


    Regular Grammar

    • 결정적 유한 오토마타(Deterministic finite automaton, DFA)
    • Regular 언어에서 오토마타는, 어떤 게 어디 속하는지에 관한 문제인 membership porblem 판별장치
    • print(FSA('aabbb')):
    derivation a*b+ Automata Grammar
    as ->
    aas ->
    aaas ->
    aaaaA ->
    aaaabB ->
    aaaabbB ->
    aaaabbb    		 S -> aS
    S -> aA
    A -> bB
    B -> b

    -S -> as | aA
    A -> bB | b

    Chomsky Hierarchy 中 Regular Grammar

    image-20200718020646135


    • 정규언어 (Regular language) 와 유한상태 인식기 (Accepted by Finite state acceptor : FSA)
    init_state = 0
final_state = [1]
trap_state = 2
delta = {0: {'a':0, 'b':1}, 
     1: {'a':2, 'b':1}}

"""
{현재상태 0 {'a' 들어가면: 다음 상태는 0, 'b' 들어가면: 다음 상태는 1}}
{현재상태 1 {'a' 들어가면: 다음 상태는 2, 'b' 들어가면: 다음 상태는 1}}
"""

def FSA(string):
  state = init_state  # 초기상태 = 0
  for s in string: 	# 'a' 들어가고 'a' 들어가고 'b' 들어가는 등 하나씩 for문에 입력됨! 
      state = delta[state][s]
      if state == trap_state: # state가 2가 되면 멈춤. 즉, 1상태에서 'a'가 들어오면 멈춤
          					# 즉, 문자열을 읽어가다가 trap state에 빠지면 reject 됨 
          break

  return state in final_state # state값이 final_state에 있으면 True, 없으면 False

print(FSA('aabbb')) # True
print(FSA('aabba')) # False
print(FSA('aabbc')) # error
print(FSA('a'))     # False


Context-free Grammar

  • Accepted by Push Down Automata, PDA

    • {a의 n승 b의 n승, n>=1}가 aaaabbbb라는 오토마타 형태(뭐다음 뭐 나와야 하고, 뭐 다음 뭐 나와야 하는 것)을 기계는 기억하지 못함. ex: N의 n승 N의 n승 -> the cat(N) the dog(N) chased(V) run(V)

  • 이때, 과거 데이터를 기억하는 오토마타의 장치: Stack

    Chomsky Hierarchy 中 Context-free Grammar

    image-20200718021947962



Context-sensitive Grammar

  • 좌우 문맥에 따라 달라지는 경우

    • S -> NP VP
    • aSb -> NP VP
    • cSd -> NP PP
    • aSb -> aS by
    • bSa -> aA bb
  • Accepted by Linear Bound Automata

  • '한글모아쓰기'에 활용되기도 함

    Chomsky Hierarchy 中 Context-sensitive Grammar

    image-20200718022925812



Unrestricted Grammar (Natural Language)

  • Recognized by Turing Machine
  • 의미는 틀려도 되고, 아무 단어나 막 조합해도 되는 것




  • 참고:

    • 아마추어 퀀트, blog.naver.com/chunjein
    • 코드 출처: 크리슈나 바브사 외. 2019.01.31. 자연어 처리 쿡북 with 파이썬 [파이썬으로 NLP를 구현하는 60여 가지 레시피]. 에이콘
© 2020 jynee